Как показали исследования [10], такой подход дает хорошие результаты. Точность данного метода достигает 0, 01 пикселя. Однако этот путь имеет существенные недостатки. Имеется в виду необходимость подбора оптимальной ширины функции Гаусса, от которой в значительной степени зависит точность определения координат хЦ, уЦ. Выбор величины 2G, в свою очередь, зависит от уровня шума, уровня квантования изображения и размеров маркированной точки. Достаточно сказать, что изменение величины 2а на 0, 5 приводит к размыванию границ на 1 пиксель. Кроме того, вычисление центра фигуры на основе (1) совершенно не защищено от влияния локального шума, наличие которого может привести к грубым ошибкам. Источником такого шума могут быть блики, тени, посторонние изображения объектов, попавшие в пределы окна с маркированной точкой и т. д.
В данной работе предлагается другой подход, основанный на использовании уравнения фигуры маркированной точки для определения координат хЦ, уЦ. В этом случае появляется возможность подавлять пиксели, принадлежащие не только общему, но и локальным шумам.
Вычислительная процедура состоит из двух этапов. Первый этап заключается в выделении границ маркированной точки. На втором этапе определяются координаты хЦ, уЦ на основе уравнения фигуры.
Выделение границ маркированной точки основано на вычислении первой производной функции изображения f(x, у). Первая производная в любой точке изображения получается из величины градиента в этой точке. Существует много способов вычисления производных от изображения. Наибольшее распространение получили способы, основанные па свертке изображения в некоторой окрестности с центром в точке (х, у) с так называемой маской (оператором) H тех же размеров. Градиент изображения G можно записать в общем виде как двумерный вектор:
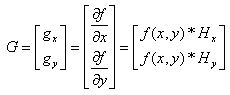 (4)
(4)
где Нx, Hy — маски;
* — обозначение операции свертки.
В качестве Нх, Ну использован оператор Собеля для окрестности 3x3:
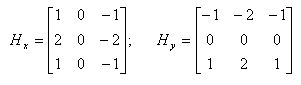 (5)
(5)
Величина градиента в точке вычисляется как
![]() (6)
(6)
Определение координат центра маркированной точки рассмотрим на примере круга:
![]() (7)
(7)
Это уравнение составляется для всех точек, имеющих ненулевые значения градиентов в пределах фрагмента изображения. Решение выполняется по способу наименьших квадратов методом последовательных приближений. Каждому уравнению присваивается вес в зависимости от величины градиента:
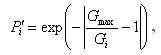 (8)
(8)
где Gmax — максимальное значение градиента в пределах фрагмента изображения; Gi — значение градиента для данного (i) пикселя изображения.
Вес, вычисленный по (8), играет роль фильтра, который подавляет энергетические шумы (порядка 20%) и сужает область пикселей, принадлежащих границе контура, которая получается размытой из-за условий съемки и преобразований (6) примерно до +/-1 пикселя.
С целью уменьшения влияния локальных шумов, соизмеримых по энергии пикселей с уровнем сигнала на маркированной точке вводится второй вес также для каждого пикселя:
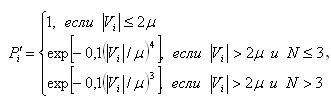 (9)
(9)
где Vi —невязка в i-м уравнении (7);
ц — средняя квадратическая ошибка единицы веса;
N — номер итерации.
Полученные таким образом координаты геометрического центра маркированной точки хц, уц на левом и правом снимках используются в качестве измеренных для дальнейшей аналитической обработки снимков, причем с весом, полученным из уравнивания.
Экспериментальные исследования данного метода подтвердили его эффективность. Координаты центра маркированной точки можно определять, в некоторых случаях с точностью 0, 01 пикселя изображения. Подробные экспериментальные исследования приводятся в следующей статье.